A hidden subset is when a number of digits only have candidates in the same number of cells. It is always complemented by a naked subset. Because a hidden subset can be difficult to find, sometimes it might be easier to find the naked subset.
Hidden Pair
When all candidates for 2 digits are contained in the same 2 cells in a house, it means that either of the digits need to be in each of the cells. Thus can all candidates for any other digits in those cells be removed.
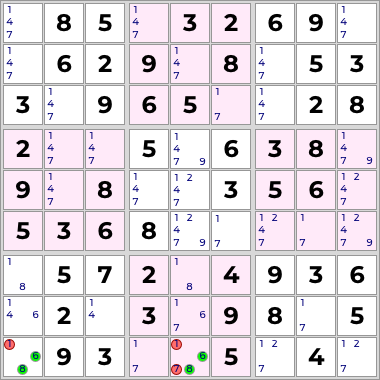
The cells r9c1 and r9c5 contain all candidates for the digits 6 and 8 in row 9, and therefore forms a hidden pair. This allows us to eliminate the candidates for 1 and 7 in those 2 cells.
Hidden Triple
When all candidates for 3 digits are contained in the same 3 cells in a house, it means that either of the digits need to be in each of the cells. Thus can all candidates for any other digits in those cells be removed. As with the Naked Triple, not all cells need to contain candidates for all 3 digits.
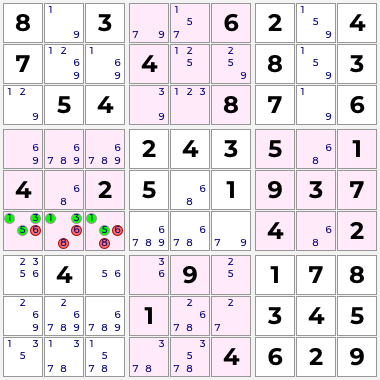
Here, the cells r6c1, r6c2, and r6c3 contain all candidates for the digits 1, 3, and 5 in row 6 (or section 4 as it is located in an intersection). This allows us to eliminate the candidates for 6 and 8 in those 3 cells.
Hidden Quad
Hidden quad is the last hidden subset, and have 4 digits over 4 cells.